编辑:Panda W
正如米爽朗基罗能用大理石雕刻出令人惊叹、维妙维肖的作品,英伟达流传宣传 Neuralangelo 天生的 3D 构造也带有风雅的细节和纹理。
对通过基于图像的神经渲染来规复密集的 3D 表面,神经表面重修已被证明是可行的。然而,目前的方法很难规复真实天下场景的详细构造。
(图片来自网络侵删)为理解决这个问题,英伟达和约翰霍普金斯大学发布了一项研究,开拓了一种命名为 Neuralangelo(即神经朗基罗)的模型,其可以将 2D ***片段重修成细节丰富的 3D 构造,比如天生建筑、雕塑和其它现实物体的逼真虚拟复制品。
项目网站:https://research.nvidia.com/labs/dir/neuralangelo/
论文地址:https://research.nvidia.com/labs/dir/neuralangelo/paper.pdf
附加材料:https://research.nvidia.com/labs/dir/neuralangelo/supplementary.pdf
这项研究已入选 CVPR 2023。英伟达在其官方博客上利用了「数字文艺复兴」来形容这项研究,足见其潜在的主要代价。
正如米爽朗基罗能用大理石雕刻出令人惊叹、维妙维肖的作品,英伟达流传宣传 Neuralangelo 天生的 3D 构造也带有风雅的细节和纹理。创意专业人士可以将这些 3D 工具导入到设计运用中,进一步编辑它们来创造艺术作品、开拓***游戏、创造机器人和家当数字人运用。
Neuralangelo 能将繁芜的材料纹理(比如屋顶瓦、玻璃板和光滑大理石)从 2D ***转译到成 3D 构造,其能力已经显著超越之前的方法。其具有非常高的保真度,让开发者和创意专业人士能更轻松地快速创建可用的虚拟工具,而所需的材料不过是用手机拍摄的一段***。
该研究的作者之一同时也是一位高等研究主管的 Ming-Yu Liu 表示:「Neuralangelo 具备的 3D 重修能力将能极大地造福创作者,帮助他们在数字天下中创建涌实际天下。这一工具终极能让开发者将细节丰富的工具 —— 不管是小型雕像还是大型建筑 —— 导入到虚拟环境中,进而用于***游戏或家当数字孪生人。」
英伟达给出了一段演示***,可以看到该模型既能重修出米爽朗基罗那著名的大卫雕像,也能重修出日常可见的平板卡车。Neuralangelo 还能重修出建筑的内部和外部 —— ***中给出了英伟达的湾区公园的详细 3D 模型。
***加载中...
下面我们来看看 Neuralangelo 的详细方法和论文中的一些实验结果。
方法
Neuralangelo 采取了实时 NGP 作为底层 3D 场景的一种神经 SDF 表征,并通过神经表面渲染根据多视角图像不雅观察进行优化;个中 NGP 是指 Neural Graphics Primitives(神经图形基元);SDF 是指 signed distance function(有符号的间隔函数)。为了充分开释多分辨率哈希编码的潜力,英伟达研究者提出了两大创造。一,利用数值梯度来打算高阶导数对实现优化稳定来说至关主要,比如用于程函正则化(eikonal regularization)的表面法线。二,为了重修出不同细节程度的构造,须要一种渐进式的优化方案。研究者将这两种思路组合到了 Neuralangelo 中,实验也证明了这样做确实可行,能极大提升神经表面重修的重修准确度和视图合成质量。
Neuralangelo 重修场景的密集构造利用的是多视角图像。它会跟随相机视角方向采样 3D 位置,并利用一种多分辨率哈希编码来对这些位置进行编码。编码后的特色会被输入一个 SDF MLP 和一个颜色 MLP,以利用基于 SDF 的体积渲染来合成图像。
数值梯度打算
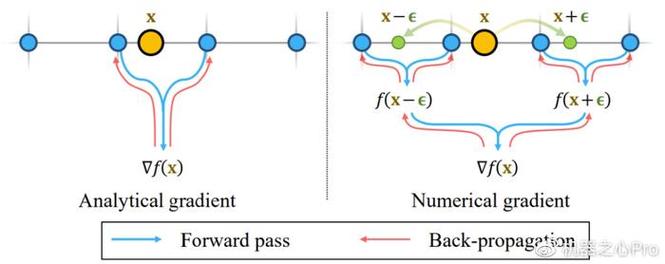
研究者表示,有关哈希编码位置的解析梯度会受到局部性的影响。因此,优化更新只会通报给局部哈希网格,缺少非局部的平滑性。针对这种局部性问题,英伟达提出了一种大略的补救方案:利用数值梯度。图 2 给出了该方法的概况。
图 2:为高阶导数利用数值梯度可将反向传播更新分布到局部哈希网格单元之外,由此变成解析梯度的一种平滑化版本。
SDF 有一种分外性子:其在单位范数的梯度方面是可微的。SDF 的梯度险些在所有地方都知足程函方程(eikonal equation)。为了迫使经由优化的神经表征成为可行的 SDF,通过会在 SDF 预测结果上施加一个程函丢失。
为了实现端到端优化,须要在 SDF 预测结果上利用一种双重反向操作。
在打算 SDF 的表面法线时,人们事实上采取的方法便是利用解析梯度。但是,在三线性插值(trilinear interpolation)下,与位置干系的哈希编码的解析梯度在空间上不是连续的。为了找到体素网格中的采样位置,须要首先根据网格分辨率对每个 3D 点进行缩放。
哈希编码的导数是局部的,即当 3D 点超越网格单元边界时,对应的哈希项将会不同。因此,前述的程函丢失就只会反向传播到本地采样的哈希项。当连续表面(比如平墙)横跨多个网格单元时,这些网格单元应该产生连贯同等的表面法线,而不该有溘然的过渡。为了确保表面表征中的同等性,须要对这些网格单元进行联合优化。但是,解析梯度却受限于局部网格单元,除非对应的网格单元恰巧能被同时采样和优化。但我们很难担保总是能够这样采样。
为了战胜哈希编码的解析梯度的局部性问题,英伟达提出的方案是利用数值梯度来打算表面法线。如果数值梯度的步长小于哈希编码的网格大小,则数值梯度就即是解析梯度;否则,多个网格单元的哈希项就会参与到表面法线打算中。
这样一来,通过表面法线的反向传播就能让多个网格单元的哈希项同时收到优化更新。直不雅观来说,利用精心选择的步长的数值梯度可被解读成在解析梯度表达式上的平滑化操作。还有另一种方法可以替代法线监督,即 teacher-student curriculum,个中要利用预测的有噪声法线来帮助 MLP 输出,这样就能利用到 MLP 的平滑性。但是,这样的西席 - 学生丢失的解析梯度仍旧只会反向传播给局部网格单元。相较而言,数值梯度无需添加网络便能够办理局部性问题。
要利用数值梯度打算表面法线,还须要额外的 SDF 样本。给定一个采样过的点,还须要在该点周围一定步长内沿正则坐标的每个轴额外采样两个点。
渐进式的细节水平
为了避免陷入缺点的局部最小值,从粗到细的优化可以更好地塑造丢失图景。这样的策略已被用于许多打算机视觉运用。Neuralangelo 也采取了一种从粗到细的优化方案来在细节上渐进式地重修表面。利用高阶导数的数值梯度能自然地让 Neuralangelo 实行从粗到细的优化,这须要考虑两个方面。
步长:前面已经提到,数值梯度可被阐明成一种平滑化操作,个中步长掌握着分辨率及重修的细节量。如果让程函丢失用更大的步长来打算数值表面法线,能在更大规模上确保表面法线的同等性,由此能得到同等和连续的表面。反过来,如果程函丢失的步长更小,就只能影响更小的区域,就能避免细节平滑。在实践中,英伟达的做法是先将步长初始化为最粗的哈希网格大小,然后在全体优化过程中指数级地降落步长以匹配不同的哈希网格大小。
哈希网格分辨率:如果从优化一开始,所有哈希网格都被激活,为了捕获几何细节,细粒度哈希网格就必须首先「忘却」粗粒度优化(更大步长)所学到的东西,并用更小的步长「重新学习」。如果优化收敛而导致这个过程失落败,那么就会丢失几何细节。因此,一开始只会激活一组初始的粗粒度哈希网格,当步长缩小至其空间大小时,会在优化过程中渐进式地激活更细的哈希网格。这样一来,就能避免「重新学习」过程,从而更好地捕获细节。在实践中,英伟达研究者的做法是在所有参数上运用权重衰减,以避免终极结果被单一分辨率特色主导。
优化
为了进一步促进重修表面的平滑性,他们还提出添加一个先验,详细做法是正则化 SDF 的均匀曲率。均匀曲率是通过离散拉普拉斯算子打算的,类似于表面法线打算,否则当利用三线性插值时,哈希编码的二阶解析梯度在任意位置都为零。
Neuralangelo 的整体丢失定义为所有丢失(RGB 合成丢失、程函丢失、曲率丢失)的加权和,如下所示:
包括 MLP 和哈希编码在内的所有网络参数都因此端到端办法联合演习的。
实验
图 3:在 DTU 基准上的定性比较
可以看到,Neuralangelo 得到的表面更加准确,保真度也更高。
图 4:定性比较不同的从粗到细优化方案
当利用解析梯度时(AG 和 AG+P),粗粒度的表面常日带有伪影。当利用数值梯度时(NG),可以得到更好的粗粒度形状,细节也更为平滑。英伟达的新方法(NG+P)得到的表面既平滑又有风雅细节。
表 1:在 DTU 数据集上的定量实验结果
可以看到,Neuralangelo 的重修准确度最高,图像合成质量也最好。
图 5:在 Tanks 和 Temples 数据集上的定性比较
比较于其它比拟方法会丢失表面细节或有较多噪声,Neuralangelo 能更好地捕获场景细节。