学得快并不能解释学得好,我在之前就提到过很多次,对付根本知识的节制,离不开习题的试炼。大概有的人说,不知道在哪找习题做,大略,你在原有的习题上练多几次,提升解题速率也不失落为一种好方法。
其余,很多时候,我们并不是学会了就完事的,而是要学甚至用,最好是能做到举一反三,例如基尔霍夫电流定律(KCL),我们学会之后就能运用到实际中,用来判断泄电保护器的接线精确与否、用来阐明钳形电流表把火零线夹在一起时示数为零的缘故原由等。

说那么多,实在目的便是要见告大家,学习是无止境的,所谓学海无涯,希望大家能跟上我的步伐,把曹老师的《电工根本》给吃透。那么,我们进入这次的主题:叠加事理。
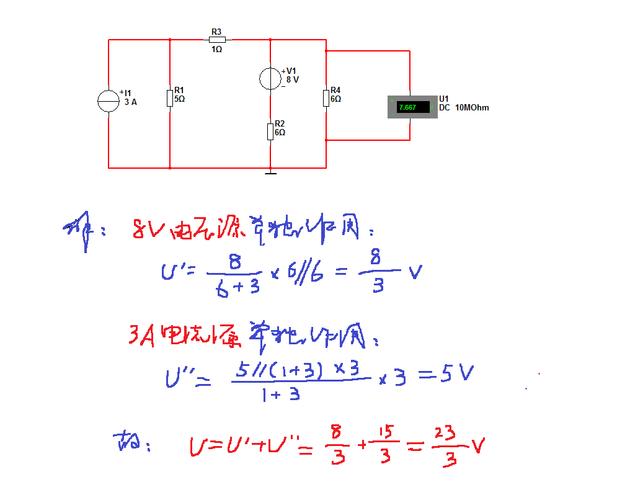
图14-1
叠加事理又称叠加定理,在线性电路中,当有两个或两个以上的独立电源浸染时,则任意岔路支路的电流或电压,都可以认为是电路中各个电源单独浸染而其他电源不浸染时,在该岔路支路中产生的各电流分量或电压分量的代数和。
作为线性系统(包含线性电路)最基本的性子——线性性子,它包含可加性与齐次性两方面。叠加定理便是可加性的反响,它是线性电路的一个主要定理。齐次性,简而言之便是输入函数增大多少倍,相应函数也会伴随着相同倍数的增大。
以是,大家要把稳,叠加定理是只适用于线性电路的。线性电路是指完备由线性元件、独立源或线性受控源构成的电路。
说到线性元件,不得不给大家说一下线性电阻,它便是线性元件,我们这次的学习也是基于线性电阻电路来讲解的。受控源在之后的学习分享中再进行详解。
线性电阻,大略来说,便是阻值不会随电压和电流的变革而变革,例如在温度不变的情形下,金属电阻元件的两端电压同电流的关系就可以认为是线性的,它的伏安特性曲线是通过坐标***的直线。
图14-2
如图14-2中,直线的斜率便是电阻的值。关于叠加定理,我们可以大略理解为日常的用水,两根水管同时接到一个水龙头,主管上的水流量便是两根支管水流量叠加所得。我们只要知道两根支管各自的水流量,主管的水流量就可以由两根支管各自的水流量相加得出。同理,叠加定理便是某处电压或电流都是电路中各个独立电源单独浸染时,在该处罚别产生的电压或电流的叠加。
图14-3
从14-1中我们可以看到,当电压源或电流源不浸染时,它们的处理方法是不一样的。电压源不浸染时是作短路处理,而电流源不浸染时是作开路处理,如下图14-3所示。当电压源不浸染时,也便是与电阻R1串联的电压源uS短路,为了便于理解,此时把电流源移到一边。
根据基尔霍夫定律(KCL、KVL),以i2为未知量来列方程,我们可以看到,原电路所得的方程与运用叠加定理求得的方程是一样的。该电路图中有两个独立电源,以是分为两个分电路,即把岔路支路电流i2分为两个分量i2’与i2’’,分别算出两个电流分量后再进行求和得出i2。
在图例中,我因此电流来展开讲解,大家在私底下可以考试测验用电压来列一下方程以加深理解,在这里就不做赘述。
叠加定理除了要把稳是线性电路外,我们还要把稳一点:原电路的功率不即是按各分电路打算所得功率的叠加,这是由于功率是电压与电流的乘积,它们不成线性关系。
我们以图14-3中的电路为例,利用功率P=I2R来证明,可以看到功率是不能直接用叠加定理求解的,如图14-4所示。
图14-4
在电路剖析中,叠加定理的运用是非常广的。在《电工根本》课程中,曹老师就以三极管的电路为例讲了一下叠加定理的实际运用,在这里也不作赘述。
利用叠加定理时应把稳以下几点:
(1)叠加定理只适用于线性电路,不适用于非线性电路。
(2)在叠加的各分电路中,不浸染的电压源置零,在电压源处用短路代替;不浸染的电流源置零,在电流源处用开路代替。
(3)电路中所有电阻都不予更动。
(4)叠加时各分电路中的电压和电流的参考方向可以取为与原电路中的相同。取代数和时,应把稳各分量前的“ ”、“-”号。
(5)线性电路的电压或电流均可用叠加定理打算,但功率P不能用叠加定理打算。
(6)运用叠加定理时,可把电源分组求解,即每个分电路中的电源个数可以多于一个。
对付第(3)点,以下图14-5为例,不浸染电流源作开路处理时,与其串联的电阻R2依然保留,不能去掉。
图14-5
而第(6)点的意思是,如果电路中含有6个独立电源,我们可以把原电路分为两个分电路,每个分电路等分别有3个独立电源或者其他分法,详细怎么分看个人需求。
至此,叠加定理的讲解就结束了,大家还有哪里不理解的呢?欢迎在评论区留言!
领取资料











