这一“二象性”的表象彷佛是:粒子图像着重局域性,将整体物理效应表达为大量粒子相互浸染的后果,即各种相互浸染力导致粒子之间的散射。此时,单个粒子动力学的描述便是核心。颠簸图像,则着重整体协同与关联,将局域物理效果表达为颠簸的叠加、干涉、衍射的后果。此时,颠簸蜕变,如振幅、频率 / 波长的蜕变动力学便是核心。从此意义上看,量子力学处理的天下,其能量尺度和时空尺度可能恰好给了粒子图像和颠簸图像“相若相合”而“琴瑟和鸣”的机会,从而使得“波粒二象性”大行其道。两者的特色,从不同侧面表现出来,让不雅观测者以为这是“粒子”或“波”。这一图像用图 1(B) 所示之经典固体波的传播来表达,最为直不雅观:您整体看是波在运动,您局域看是一个粒子在运动。
如此不雅观念,并非一定要在量子力学中才能被清晰而严谨地表达。生手如 Ising 者,这里有点要抬杠的意思^_^!
量子力学作为革命性理论,个中一些不雅观念也可借用到经典物理和数学上,作为朴素表达的一种“思辨”。如此这般的马后炮式牵强附会,是 Ising 的强项。读者不妨放弃严格和较真的态度,姑且看看 Ising 就其较为熟习的几条横道竖理,说出个一二,以判断“颠簸”与“粒子”共存在科学内涵上是否有迹可循。

(A)
(B)
图 1. (A) 量子力学所要表达的“波粒二象性”:空间传播是颠簸 (物质波),而能量行为是粒子 (准粒子)。(B) 经典固体中波的纵向和横向振动传播,个中玄色方块表达一个所谓的“粒子”。
(A) from https://factmyth.com/factoids/light-is-both-a-particle-and-a-wave/。(B) from
https://www.mtu.edu/geo/community/seismology/learn/seismology-study/body-wave/。
Ising 无所事事之余,之以是想诡辩这种视觉,乃是以为凝聚态物理中的征象学相变过程、或者说朗道对称性范式下的对称性破缺、亦或说量子材料中各种量子态的产生泯没 / 共存 / 竞争过程中,颠簸作为媒介要更“随意马虎”、更长于“妥协”、更趋于“逐渐” (韶光长一些),所需能量也就更低。而粒子化模式 (详细而言,如“成核终年夜”过程),则表现得更 sharp、革命化、tough 化,须要更高能量引发,但一旦发生却更快、更溘然。读者可看到,Ising 这里的表达很大口语!
也因此,量子材料中那些通过对称破缺、成核终年夜等高能过程而实现有序态的物理效应,个中可能隐含有一些未曾被揭示的、更“颠簸”的物态。借助得当的量子材料,去“显示”这些物态,该当很 exciting 和 high?!
不信,来看几个例子:
(1) 首先,看高档数学。对一局域几何形状,例如 xy 坐标系中一个矩形,当然可以用一个局域函数 (数学表达式) 来描写,如图 2(A) 所示。这种局域、粗暴描述的不雅观念,大约便是“粒子化”的模式。而学过微积分的人也知道,用一个傅里叶级数或三角函数级数,可以无限趋近这一形状。这些级数的每一项是什么呢?可算作是具有特定频率 / 振幅的波。这些波在全体坐标系中叠加,即“堆叠”出这一局域的矩形形状。这彷佛也是整体的波和局域的粒子间一种等价性。Ising 当年学习微积分和级数展开时,隐约感想熏染到这种不雅观念,并在后来的博士论文中半推半就利用过。物理人彷佛很早就考试测验用“波”及其叠加来描述任意一个几何工具,这不便是“任意一物体既是粒子也是波”的意象么?
(2) 其次,看凝聚态中热力学相变。那些归属于朗道对称性破缺的相变,彷佛可用粒子和波的不雅观念分别去描述,有殊途同归之意。以一级相变为例,有“成核成长 (nucleation & growth, NG or binodal)”和“调幅分解 (spinodal decomposition, SD)”两类模式,如图 2(B) 的相图所示意:
(A) 降落温度,从母相中形核、终年夜而形成新相,大量新相在母相中终年夜而耗尽母相或到达两相共存,是通过 NG 模式完成相变的图像。这里,新相胚胎很像是个粒子、是局域的,须要构造和身分大幅度涨落而超越较高势垒达到新相。
(B) 降落温度,从母相通过调幅分解 SD 模式逐渐蜕变,形成新相。这一过程的振幅和波长蜕变是渐进式的 (图 2(B) 中 SD 区域内插入了空间浓度波的蜕变进程),直到末了阶段才耗尽母相或到达两相共存。熟习 SD 的物理人都知道,SD 多是热力学自发进程、无需战胜能垒,或只需很小驱动力便可进行。这一过程,是一种颠簸,一开始由一系列幅度无穷小、波长随机的涨落组成。随韶光延长,波长竞争而完成择优选择,继而振幅增强和模式软化 (即频率变慢,即调幅波不断软化并终极走向波长发散的过程,俗称软模冻结)。
因此,热力学相变,可理解为是粒子图像 (成核成长) 和颠簸图像 (调幅分解) 交替并行的“二象性”。虽然教科书说一个体系只能在 NG 或 SD 中取其一,但实际上两者本便是共存联动的。一级相变那个著名的 Cahn – Hillard (CH) 动力学方程,实质便是颠簸的,其解也可以是颠簸叠加的形式。CH 方程将母相 – 新相界面处理成弥散连续几何,将本以为是分离的 NG 和 SD 两种模式席卷个中,让三十年前的 Ising 很受震撼、并留下深刻印记。
有了这“首先”和“其次”的鼓励,Ising 便可更放荡地臆断这一扩展的“二象性”还真是那么回事。拓展到二阶相变,亦可牵强遐想几个例子。
图 2. 经典相变物理中粒子与波“二象性”的征象学表达。
(A) 一个局域的矩形总可以被一系列傅里叶波叠加而无限近似,个中不同振幅和波长的波用各种颜色的颠簸曲线表达。(B) 二元合金一级相变的相图,外侧类弧线表达形核成长 NG 的临边界,绿色的颠倒类抛物线表示调幅分解 SD 发生的临边界 (SD 区域内还插入了一支调幅波的波幅随韶光蜕变三个阶段:early, later, final)。下部展示了合金相变著名的 CH 方程及其微积分表达。(C) 铁电材料中一个顺电相构造单元 (右) 通过对称破缺形成一个电偶极子 (左),既铁电“粒子”单元。(D) 安德森的铁电软模理论图像,个中横光学波对应正负电荷相向振动,在波长趋于无穷 (波矢 q 减小到零) 时对应横光学模冻结 (即频率 ω 趋于零),导致长程铁电电偶极子序。(E) 教科书中展示的自旋 (或矢量) 涡旋 – 反涡旋对,是一种低能颠簸引发。(F) 自旋波的构造,也是自旋低能颠簸引发。
(3) 再次,是铁电相变。铁电相变可归于二阶,也有人将其归于弱一阶。这不主要,主要的是,传统铁电理论依然从朗道对称性破缺框架展开。一个电偶极子,如图 2(C) 所示的一个晶格单元,就像一个粒子。粒子相合耦合而有序排列成铁电畴,是范例的成核成长“粒子”图像。昔时夜神安德森的追随者转头看他老人家提出的软模理论时,“颠簸”图像也油然而生。铁电软模,如图 2(D) 所示,便是晶格光学横模声子蜕变的进程。其振幅不断增强、频率不断减小,及至末了频率趋于零。声子模软化冻结,形成电偶极子畴,实现铁电相变,虽然是很受物理人喜好的安德森物理,但材料人更欣赏顺电相中成核成长完成铁电相变的图像。孰是孰非、未置可否,也是“二象性”的某种表示。Ising 以为,声子软模更多是经典成核模式的一种颠簸表述,它们是一件事情的两幅面孔。
(4) 以磁性相变为例来结尾。Ising 对磁学是生手,但也知道顺磁母相中形成铁磁 / 反铁磁新相时,NG 模式大行其道。只是,如果磁晶各向异性不那么强,vortex – antivortex (V – AV) 模式或自旋波 (spin – wave, SP) 模式亦可展现,如图 2(E) (V – AV) 和图 2(F) (SP) 所示。通过波长蜕变和颠簸模式软化而形发展程磁性相,此中物理彷佛类似于、却比铁电中的“二象性”更丰富和宽阔,在此不论,以避免坐井观天。
举例这么多,读者可能被糊涂了:到底要干什么!
Ising 重复之、归纳之,大概有如下几点:
(a) 所谓的波与粒子的“二象性”,并非一定是描述一种效应的两种机制,也可以是这一效应的两幅面貌,即 duality。
(b) “颠簸”效应看起来须要的局域能标较小 (亦即须要的单位体积的能量较小),因此在驱动力较小时优先涌现,但动力学上较为缓慢。支持这一议论最好的证据,乃来自量子磁性中的自旋波低能引发,如图 2(F) 所示:必须是自旋波,而不是其它!
而“粒子”效应,不那么随意马虎显现,更无须强调所涉及的对称性破缺问题。
(c) 如果驱动力足够大,“颠簸”机制就可能被粉饰掉,能标较大的粒子机制就会胜出。毕竟,粒子机制是局域的,只需局域内身分或构造的涨落足够大即可,且所需韶光尺度会很短。波动机制,须要整体协同、叠加,能标大概很小,但需更永劫光蜕变。
如上三条,果若碰着得当的系统,就可演绎出新物理来。这一理解,彷佛在量子材料中展现得更为显著。特殊是个中的超导物理,这样的实例信手拈来。不妨再去看已被量子材料人看烂了、谈论烂了的非常规 d 波铜基超导相图,如图 3(A) 所示。由于强电子关联效应,这里原来能标很高的载流子动能项被电子关联大幅抑制,给了多少小能标“颠簸”态以登堂入室的机会。例如,物理人很早就知道,电 – 声子耦合物理,除了驱动电子库珀对外,也能引发“电荷密度波 CDW (charge density wave)”、“配对密度波 PDW (pair density wave)”之类。电子关联还可能导致自旋涨落一类的电子配对模式,副产品也有“自旋密度波 SDW (spin density wave)”、“电子向列相”之类。相图中环绕在超导区四周的那些量子态,都或多或少与“颠簸”有联系。对其它类别的非常规超导,类似的定性议论也是适用的,只是不那么范例,在此不再絮叨,仅仅列举铁基超导的相图一幅如图 3(B) 所示。
图 3. 铜基超导相图 (A) 和铁基超导相图 (B)。可以看到,在超导相区四周都是一些“颠簸”相,如 CDW、SDW、PDW、Nematic state 等。
(A) From B. Keimer et al, Nature 518, 179 (2015),
非常规超导相图的这些“颠簸”特色,给物理人一种印象:CDW、PDW、SDW 等这些“波”,该当是非常规超导的内在属性:只要压制那些高能标的物理过程,如引入强关联去压制动能项,超导体系就可能衍生出与电子超导配对“牵扯不清”(竞争、共存或相关) 的、具有“颠簸”属性的物理、物态。这样的物理,在铜基超导、铁基超导、魔角超导、乃至是才涌现的镍基超导中,彷佛都若隐若现、宛若江湖传说一样平常!
揭示并操控它们,是超导物理人的宿命,否则他们就得“曾经沧海难为水”了^_^!
稍等!
真的必须要非常规超导么?常规超导中,或者干脆说电 – 声子耦合主导的超导中,难道就没有这些“颠簸”属性的舞台了?
这样的问题,最近就被人提及,并被认负责真地磋商了一番。被磋商的意义,Ising 以为有两个层面:(1) 常规超导中有否低能标的“颠簸”物态什么事?又是什么事?(2) 如果有,传统超导物理能不能展现其存在?这样的意义,不能说是天算夜的物理,但也是很主要的物理。
呈现这一意义的超导体,实在就在面前,即最近几年备受关注的钒基笼目超导体 (kagome metal) AV3Sb5 (A = K, Rb, Cs),其晶体构造和超导相图显示于图 4(A) 和 4(B) 中。这一笼目材料种别,乃由米国加州大学圣巴巴拉分校的帅哥 Stephen D. Wilson 小组创造,随即引发量子材料领域同行高度关注,包括超导电性、CDW、PDW 等“颠簸”物态,也纷纭被确认和深入磋商。特殊指出,我国学者在这一领域成绩斐然,包括中科大陈仙辉老师、中国科学院物理所胡江平老师在内的诸多有名团队都很有建树,如仙辉老师他们关于 CDW、江平老师他们关于局域自旋反演破缺调制 (手性磁通相 chiral flux phase, CFP) 等结果。2022 年,江平老师他们曾经在《物理学报》期刊中刊发过一篇对这一主题的科普总结 (https://wulixb.iphy.ac.cn/article/doi/10.7498/aps.71.20220891),非常棒!
感兴趣的读者可前往御览阅读,Ising 在此不再絮叨。
图 4. 具有 kagome 晶格的无磁性金属化合物 AV3Sb5 之构造 (A) 与量子态相图 (B)。故意思的是,一旦进入超导区域 (无论 V – shaped 还是 U – shaped 区域),高温区形成的 CDW 和其它“颠簸”涨落都全数泯没、不复存在。这与非常规超导体的超导相区内非常“不干不净”的结果大相径庭。
(A) From H. X. Li et al, PRX 11, 031050 (2021),
(B) From H. Yang et al, Science Bulletin 67, 2176 (2022),
具有 kagome 晶格的 AV3Sb5 金属,就具备如上提及的“被磋商之意义”:
(1) kagome 点阵,更多是一类准二维的晶格,由六边形和三角形交替嵌套而成,其面内平移对称性很低,大大压缩了高能标物理的可能性。如此,载流子要在面内迁移就很困难,导致明显的所谓“平带”效应。这,很像魔角体系中的 Moire 条纹晶格,也具有强“关联”或“平带”物理!
(2) 这类体系不含磁性元素,轨道磁矩也无多少非同平凡。针对 AV3Sb5 超导电性的诸多研究,彷佛都指向一个共同结论:这是一类 s 波常规超导!
彷佛 BCS 理论或归于此类的电 – 声子超导理论模型,应可用来描述个中的物理,包括诸如 Holstein model 这样的理论模型。
(3) 既然无磁性、是 kagome,体系中涌现小能标“颠簸”物态并不稀奇。也便是说,个中涌现 CDW、PDW 等与超导竞争的“波”物理或“颠簸”态,彷佛也情有可原。但是,诸如 Holstein model 这样的经典模型,真的能给出这些个“情有可原”么?
回答这一问题,不是件随意马虎的事,但亦有好此之物理人。来自米国加州大学戴维斯分校的理论凝聚态学者 Richard T. Scalettar 教授领导的团队,与来自米国田纳西大学和洛斯阿拉莫斯国家实验室的团队互助,对此展开了探索。Ising 非物理人、更非超导理论物理人,即便是抱着 Scalettar 教授他们最近刊发在《npj QM》上的理论大作读了良久,依然未能窥得个中分毫。不过,他们的文章写得很洒脱而清晰,生手多看几遍,亦可看出一点热闹。他们的事情大意如此:
(a) 既然 kagome 体系如 AV3Sb5 (A = K, Rb, Cs) 非磁性、展现的多是 s 波超导物理,为何个中会有常规超导中不常见的 CDW?大量实验和理论谈论,都确认了 AV3Sb5 中的 CDW。那么,一个范例的电 – 声子耦合模型,就该当能容纳 CDW,不是么?
(b) Holstein model 是传统超导物理中用于描述电 – 声子 (Einstein phonon) 耦合、既大略又范例的模型,曾被广泛研究、并被拓展去描述非常规超导中的电 – 声子相互浸染物理 (考虑关联后,即那个著名的 Hubbard – Holstein 模型)。大略又著名,解释其拽着了常规超导体系中电 – 声子耦合的关键。而电 – 声子耦合,又是 CDW涌现的根源之一。
(c) Holstein 模型已被成功用于预测诸如正方点阵、蜂窝点阵和 Lieb 点阵中的 CDW 和超导电性。现在,该轮到 AV3Sb5 这一 kagome 金属体系了,且它亦是 s 波常规超导体系。去看一看这一模型能否捕捉到 kagome 点阵中 CDW 的踪影,无疑是有代价并令人迫不及待的题目!
(d) 果不其然,Scalettar 教授他们利用最近发展出来的殽杂蒙特卡洛仿照方法 (hybrid Monte Carlo simulation),揭示出该点阵存在 3 × 3 的 CDW 有序态,虽然这一有序态只涌如今电子添补浓度 (average electron filling) <n> = 2/3 的固定点处。他们的部分打算结果显示于图 5 中 (详细描述拜会原文)。更进一步,他们还估算了 CDW 涌现的温度。结果是,温度与电子动能项成正比,但却很低。大量的搜索打算显示,在任何其它 <n> 和高温区,都无 CDW 的踪影。看起来,CDW 在这一模型中有稍纵即逝的味道。
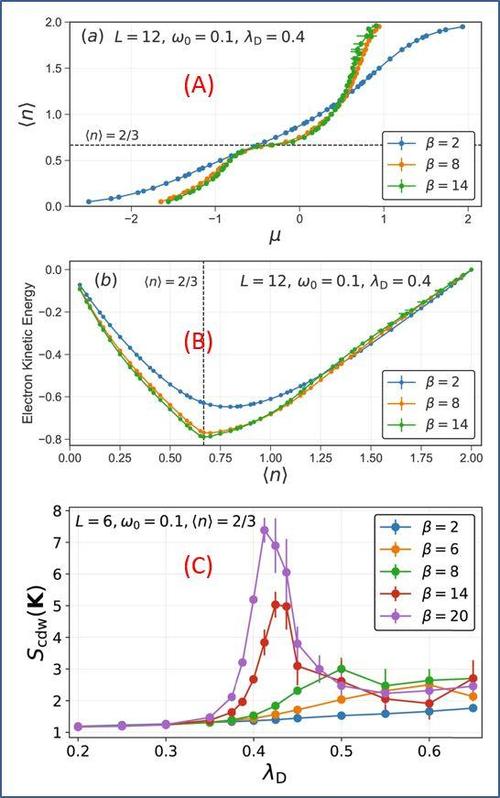
图 5. Scalettar 他们针对 kagome metal 晶格,从 Holstein 模型出发,基于 hybrid Monte Carlo simulation 得到的紧张结果。
(A) 特定参数空间中,不同温度 (1 / b) 下均匀电荷密度 <n> 与化学势 μ 的关系,清晰展示出在 <n> = 2/3 处存在平台区,对应于 μ ~ – 0.5 处。(B) <n> = 2/3 处电子动能处于最小值,意味着 CDW 的确会涌现于此。(C) 打算得到的 CDW 构造因子 SCDW 与电 – 声子耦合强度 λD 的关系。很显然,μ ~ 0.4 时,构造因子 SCDW 涌现敏锐峰值,证明 kagome 金属点阵模型体系中是可以涌现 CDW 的,令人印象深刻。
所有这些模型谈论与仿照结果,显示出 CDW 这个“波”涌如今 Holstein model 中是不随意马虎,但不是不可能。给定 kagome 金属、给定 AV3Sb5,也可以形成 CDW,令人感想熏染到电 – 声子耦合和超导物理是多么善于“川剧变脸”、多么随意马虎“人面桃花”而“波粒二象”。就这一点,该项理论事情是有一定意义的,并提示物理人:常规 s 波超导中也是可以有很多好物理的。阿门!
雷打不动的结尾:Ising 乃属生手,描述不到之处,敬请包涵。各位有兴趣,还请前往御览原文。原文链接信息如下:
Charge order in the kagome lattice Holstein model: a hybrid Monte Carlo study
Owen Bradley, Benjamin Cohen-Stead, Steven Johnston, Kipton Barros & Richard T. Scalettar
npj Quantum Materials 8, Article number: 21 (2023)














