|作者:朱健凯 徐博 王曾晖
(电子科技大学根本与前沿研究院)

本文选自《物理》2024年第2期
摘 要
纳米机电器件是具有机器运动自由度的纳米电子器件。特殊有趣的是,纳米机电器件同时也构成了微纳天下的各种乐器,能够演奏出独特的音乐之声。犹如宏不雅观天下中的乐器各有各的特色,这类微纳器件在研究低维及纳米尺度的物理征象时,也展现出一些独到的潜力和上风,例如研究低维体系中的独特相变过程以及纳米材料中的力学各向异性效应等。在这些事情中,通过精密丈量低维纳米材料的机器振动,即仔细谛听这些乐器所奏出的音乐之声,能够帮助研究者们不雅观察到一些原来不易被丈量的征象,进而探索新的低维物理过程和材料体系,带来新的科学创造。
关键词 纳米机电器件,低维纳米材料,音乐
1
引 子
纵不雅观科学史,会创造不少著名的科学家都有一项爱好:演奏乐器。在外国科学家中,爱因斯坦演奏小提琴的照片早已广泛流传,而费曼则以喜好玩爵士鼓而著称。对付这一情形,大家可能以为不足为奇,毕竟不少科学家从小就接管了良好的家庭教诲,以是会演奏一些乐器也不奇怪;而科研事情每每比较辛劳,以是他们在事情之余通过演奏乐器来放松自己,调处一下也实属正常。
然而,对付科学家来说,音乐是否只有放松和熏陶情操的功能呢?音乐与科学之间,是否还有更紧密的联系?一方面,大家都知道乐器的事情事理会涉及到一些干系的物理知识,例如振动和波;另一方面,音乐和乐器是否也能对科学研究带来启示,促进物理学的发展呢?
本文将从这个角度出发,先容一类特殊的乐器——“原子尺度的乐器”。通过磋商它们的演奏过程以及和不同成分的相互浸染过程,来一窥微纳天下的“音乐之声”,并借此探索有趣的物理征象。
2
乐器,可以有多小?
原则上,能够发生发火声音的物品都可以称为乐器。发生发火声音一样平常是由空气振动引起的,这种振动以波的形式传播到听众的耳中。对机器振动而言,最基本也是最大略的形式是简谐振动,也便是恒定幅度、单一频率的周期性运动,在很多物理教材中都有涉及。在单一自由度下,其含时位移的表达式为
式中,是振幅(即振动过程中达到的最大位移),是振动的频率(即振动周期的倒数),为初始相位。频率是一项最关键的参数,对应于音乐中的腔调。绝大多数乐用具有频率选择的功能,从而发出特定腔调的乐声。从实现频率选择的角度,乐器大致可以分为两类。第一类自身并不振动,而是给空气供应一个振动并形成驻波的环境,如风琴、笛子等,通过改变振动段空气的长度,来改变乐器中空气共振模式的频率。声速不变情形下,长度决定了稳定驻波模式的波长也就决定了频率。第二类乐器则更为常见,通过自身构造(例如一维的弦,二维的膜)的振动来引发对应频率的声波在空气中传播,频率的选择通过乐器的自身构造实现,如琴弦的长度,鼓膜的大小等等。为了方便演奏过程中高效的频率选择,后一类乐器每每由一系列的振动部分组成,如钢琴上是非不同的琴弦,架子鼓中大小互异的鼓面。在声波开始传播之初,振动(驻波)就已经存在于乐器自身构造中。与前一种乐器类似,振动部分的尺寸越微缩(琴弦越短或者鼓面越小),腔调每每越高(声速一定,驻波模式的频率与尺寸成反比)。理论上,只要把乐器的振动部分不断缩小,就可以把腔调“无限”提高(当然音量也每每随之减小),一贯进入超声乃至更高的范围。
按照这样的规律,人们可能会追问,乐器可以一贯缩小下去吗?频率可以无限提高吗?当“乐器”小到一定尺度,会涌现新的物理征象吗?从某种意义上来说,目前人类能够实现的固体是由原子构成的,以是绝大多数的人造构造都受到原子极限的制约,由此可以认为原子尺度的“乐器”代表了乐器微缩所能达到的一个比较主要的极限。
那么,如何才能将乐器不断朝着微纳尺度微缩,靠近乃至达到原子尺度这一极限呢?说来也巧,上文提及的费曼,曾经有过一段非常著名的论述“There is plenty of room at the bottom(微不雅观天下乃广阔天地)”,被认为是微纳科学领域的开山之论。在过去的几十年中,微纳加工技能和纳米材料成长技能得到了长足的发展,使得微纳乃至原子尺度“乐器”的实现成为了可能。目前,这类构造在科研领域最常见的称谓是“微纳机电系统/器件”(micro/nanoelectromechanical systems,M/NEMS),以突出其机器运动的自由度。下面本文将以原子尺度的“琴弦”和“鼓面”两种振动构造为例,大略先容微纳机电器件的制备过程。
图1 一维和二维纳机电谐振器示例图 (a)悬空的一维纳米管(图中箭头所示),类似于琴弦;(b)悬空的二维晶体薄膜,类似于鼓面
对付具有一维“琴弦”或二维“鼓面”的乐器而言,它们最核心的功能部位是能够产生机器振动的微纳构造,而根据微纳构造的形状(如长宽比等指标)可将其分为一维和二维构造(图1)。到目前为止,一维构造的最小直径可以缩小到1 nm以下,如单壁碳纳米管(carbon nanotubes,CNTs),而二维构造最小的厚度能达到单个原子层,如单层石墨烯。器件尺寸微缩到原子级的发展现状,也意味着材料合成和器件加工都面临着相应的寻衅。通过研究者们的探索,目前形成了两条紧张的制备路子,其紧张差异在于纳米构造制备的末了一步是“减材”还是“增材”。
图2 低维纳机电谐振器制备方法举例 (a)末了一步“减材”的方法:从非悬空的纳米管开始,通过刻蚀移除纳米管下方的材料使其悬空;(b)末了一步“增材”的方法:提前加工好悬空所需的构造,末了一步将纳米材料转移到预制好的构造上,形成悬空的纳米构造
这里以类似琴弦构造的一维碳纳米管谐振器为例,大略先容一下制备流程。第一种方法是在衬底上成长碳纳米管,然后在加工制备微沟槽时进行精确定位,对准所选的碳纳米管下方进行衬底刻蚀,从而实现悬空的纳米管(图2(a))。另一种方法则是预先准备好微沟槽等构造,在末了的制备步骤中将纳米管以悬空的办法成长或转移至沟槽处(图2(b))。后者的优点在于纳米管始终不与各种有机溶剂打仗,具有非常干净的表面(无需额外的化学处理),还可以实现非常长(毫米级)的碳纳米管谐振器。
与一维“琴弦”类似,二维“鼓面”的制备方法也可以大致归为这两类。早期,人们利用“减材”的第一类方法实现了二维带状谐振器,构造有点类似于木琴:振动部分比琴弦要宽(薄片状),但又不似鼓膜那样是四周固置的。在此根本上,利用聚合物在二维薄片周围构建支撑构造可形成一个四周都固定的谐振器,就与鼓面非常类似了,还可以规模化制备,实现谐振器阵列。利用“增材”的第二类方法,人们通过剥离二维材料到预制孔洞的衬底上,可以实现“鼓面”构造,并在此根本上开拓了定点制备技能和水赞助转移的大规模制备技能。
总而言之,微纳尺度的“乐器”加工,涉及到了过去几十年各学科的技能发展,也从费曼时期的“异想天开”逐渐变成了本日实验室中越来越丰富多样的现实存在。
3
微纳尺度上的乐器演奏
“乐器”造出来之后,一个自然的问题是如何去“演奏”。宏不雅观尺度的乐器自然可以靠人力演奏,但原子尺度的乐器显然须要不同的“演奏”方法,来勉励微纳尺度的机器振动。下面就大略先容一下微纳机电器件中机器振动的勉励过程。
3.1 电学勉励
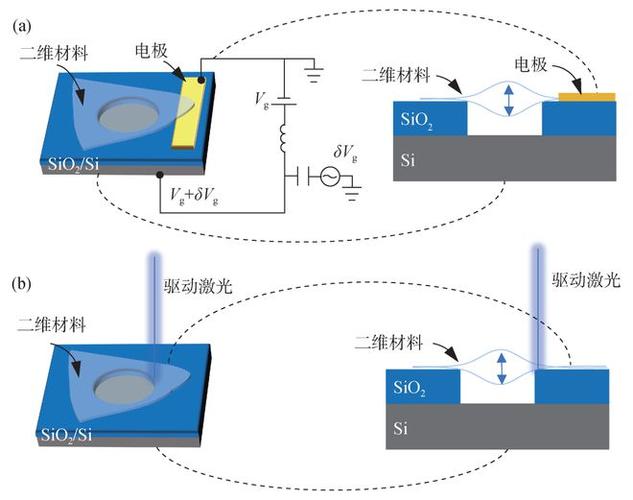
电学勉励是微纳机电器件研究中广泛运用的一种勉励办法,个中以电容式静电勉励最为常见(图3(a))。器件的悬浮构造(“琴弦”或“鼓面”)和基底栅极的关系可以等效为电容构造的两极。通过在栅极上施加一个交变电场,就会产生一个交变的电容力,可以为乐器振动供应周期性的驱动。当驱动频率与乐器的固有频率相同时,乐器的相应(受迫振动)会涌现最大振幅,即发生共振。
图3 二维纳米机电系统机器振动的勉励 (a)静电勉励的示意图:通过在二维鼓膜和下方电极之间施加交变电压来产生周期性的驱动力,从而勉励鼓膜高下振动;(b)光热勉励的示意图:通过调制照射到样品上的光强来产生周期性的光热力,从而驱动鼓膜振动
3.2 光热勉励
光热勉励是微纳机电器件中另一种紧张的驱动办法(图3(b)),依托光强被调制的激光对材料进行周期性的加热,该方法对材料导电性无分外哀求,适用于h-BN谐振器等电学勉励较为困难的器件。此外,由于不须要对器件加载电流、电压旗子暗记,大大降落了器件构造设计的哀求。因此,光热勉励非常适宜新型二维谐振器的初期研究,以及新器件振念头能的探索实验。
3.3 其他勉励
除了光学和电学外,还可以采取磁力驱动、机器驱动等方法。有趣的是,当微纳器件中的一个维度扩展到宏不雅观尺度时(如超长碳纳米管这种又细又长的“琴弦”),直接施加声波即可实现勉励,在这个意义上也彰显了其“乐器”的实质。
4
聆听微纳尺度的“乐声”
“乐器”演奏起来了,下一个问题自然是如何“听”到“乐声”。宏不雅观尺度乐器振动的频率在人耳的听力范围内,乐声通过空气中的声波传播。但原子尺度乐器对应的频率远远超过了人类乃至所有动物的听力范围,而且振动每每在真空环境下发生,无法通过空气来传播机器振动波(如此高频率的振动也远远超出了空气可以传播的范围)。以是,须要采取不同的方法,来“听见”微纳尺度的音乐之声。下面就大略先容一下微纳机电器件中机器振动的读取过程。
4.1 电学读取
由于微纳器件的运动构造尺寸极小,且微纳器件的电极尺寸比悬浮构造大几个数量级,导致电路中存在较大的寄生电容,器件的振动旗子暗记很随意马虎淹没在电路的寄生旗子暗记中。因此,研究者们开拓了混频技能:以石墨烯鼓膜谐振器(石墨烯扮演“鼓面”的角色)的双源混频丈量为例(图4(a)),在器件栅极施加频率为的旗子暗记,同时在漏极施加频率为+Δ的旗子暗记(Δ一样平常在kHz)。这里谐振器扮演混频器的角色,将两路射频旗子暗记进行混频,器件机器振动的信息被调制到频率为Δ的低频旗子暗记上,终极通过锁相放大器对源极输出真个旗子暗记进行锁相处理即可提取。该技能的核心思想是:既然正面打破不成(寄生旗子暗记紧张在高频段),那就“借道”而出(将振动旗子暗记调制到低频载波中),有效避开了高频寄生旗子暗记的滋扰。
图4 二维谐振器电学读取示意图 (a)双源混频丈量:在栅极和二维薄膜上施加频率略有差异的射频旗子暗记,并利用谐振器作为混频器;(b)直接读取丈量:通过抑制寄生旗子暗记,无需混频即可直接读取出器件的振动旗子暗记
在详细研究中,调幅和调频技能均可用于简化电学混频读取,并起到和双射频源类似的混频效果。除此之外,研究者们也努力通过优化器件构造实现谐振旗子暗记的直接读取(图4(b)),例如引入局部栅极来减少寄生电容。
4.2 光学干涉读取
无论是为探求“以太”而设计的迈克尔孙—莫雷干涉实验,还是为捕捉引力波而搭建的LIGO不雅观测站,激光干涉都作为精密丈量的核心部分运用个中,并取得了科学史上的卓越造诣。同样地,当光学干涉运用于微纳机电器件丈量时,可以成功地检测到pm乃至fm级的机器振动。
这里以鼓膜谐振器的干涉丈量为例(图5):当激光入射到器件上时,在鼓膜的上表面、下表面,以及下方衬底表面均会发生反射乃至多重反射,终极形成多组彼此干涉的反射光,可以将器件位移转换为光强变革,再通过光电探测器的吸收和放大得到电旗子暗记。
图5 二维谐振器光学读取示意图。个中,蓝色激光用于光热驱动,赤色激光用于器件位移的干涉丈量。从器件反射的光旗子暗记携带振动信息,被光电探测器转换为电旗子暗记后可以被不同的设备读取
光学干涉读取相较于电学读取紧张的上风表示在无需为器件设计并制备相应的电极构造,对悬浮材料导电性亦没有任何哀求。更主要的是,由于光学干涉法能丈量到鼓膜上每个位置的振动信息,因此这一技能可以运用于微纳器件振动模态的可视化,类似于用高速摄像机拍摄得到乐器振动时的真实描述(见下文5.2中的例子)。通过可视化的呈现,这些纷繁繁芜的模态展现了“鼓面”对人们演奏(勉励)的反馈:不同的勉励频率下,“鼓面”呈现的振动各不相同。这类似于用不同的速率去搓鱼洗(鱼洗是我国古代的一种金属盥洗用具,形似现在的脸盆,两端有柄,称作“耳”)可以在水面形身分歧的纹理。
4.3 其他读取办法
除了电学和光学读取技能外,磁力检测、原子力显微镜、扫描电子显微镜、透射电子显微镜也被用于一维和二维纳米谐振器的振动检测。
5
微纳尺度的乐器与物理
当人们能够“演奏”这些原子尺度的乐器,并可以在微纳天下中“听到”它们发出的“音乐之声”时,是否可以用它们来研究一些新奇的物理征象呢?答案是肯定的。下面通过原子尺度的“琴弦”和“鼓面”的两个实例,对这个领域的研究略作先容。
5.1 用原子尺度的琴弦来研究低维相变过程
相变是一个主要的物理过程,在日常生活中也随处可见。例如,冰融化成水再蒸发成水蒸气,这一最常见的固液气相变,对地球上生命的涌现起到了至关主要的浸染。然而从物理学的视角,相变还存在着一些根本的问题有待办理,个中就包括了维度的影响:当物质体系从三维变成二维或更低的维度时,相变征象是否会改变;乃至,在低维下是否还会存在相变?
针对这个问题,实验上的寻衅是显而易见的:若何找这样一个物理体系,能够确保其纵然发生相变(例如气化),所有的原子仍旧留在同一个二维平面内呢?幸运的是,物理学家还真的找到了这样一个实验系统:单层吸附体系。人们创造,一些层状晶体如云母、高定向热解石墨(HOPG)在解理时可以涌现较大面积原子级平整的表面,可以作为较为空想的吸附衬底。
通过掌握温度和环境压强,人们在HOPG上实现了多种单原子层的吸附体系,即吸附的量恰好构成一层原子的厚度。通过对吸附单原子层采取成像(如STM)、散射(如电子、X光、中子等)、热力学方法(体积/气压法、热容法)等实验手段进行研究,人们在这类二维体系中成功地不雅观测到了(类比于三维体系中的)固、液、气等一系列二维相,以及相变、临界征象等物理过程。
探索了二维体系的相变后,人们自然地把目光转向了一维体系。而在实验体系的选择方面,人们想到了当时刚刚涌现的一维纳米晶体:碳纳米管。单壁碳纳米管可以想象成是一段石墨烯窄带无缝地卷成了一根苗条的空管,具有六边形碳环构成的无毛病表面,很小的直径(可以少于1 nm)以及极高的长宽比(长度和直径之比可以达到10乃至更多),被认为是非常靠近一维的物理体系。因此,如果能在单根碳纳米管的表面构建一个吸附的单原子层,就可以为人们研究相变过程从二维向一维的蜕变供应一个平台。
虽然这一思路听起来较为可行,且有前期大量HOPG的实验可以供应借鉴和支撑,但是在实际研究过程中人们创造了一个关键的问题:单根碳纳米管上吸附体系的丈量极具寻衅。比较之前的吸附体系,单根碳纳米管的总表面积小了8—10个数量级(毫米尺寸HOPG样品的总表面积一样平常是10—10m,但微米长度的碳纳米管总表面积只有10—10m),因此可丈量的旗子暗记强度也相应地大幅减弱,原有的实验手段均难以适用。
在办理这一寻衅的过程中,乐器给人们带来了独到的启示。设想一根琴弦,在张力一定的情形下,其腔调(振动频率)与质量密度直接干系,这也是为什么在吉他等乐器上,线质量密度越大(一样平常也是越粗)的弦被用来演奏更低的腔调。如果琴弦的质量密度发生变革,其腔调也会发生相应的变革。以是,如果人们能够将一根碳纳米管当作一根振动的琴弦并监测其腔调,就可以不雅观察到其上吸附层在相变过程中发生的质量密度的变革。
沿着这一思路,人们通过前文所述的微纳加工方法,制备了基于单根碳纳米管的纳米琴弦,并采取振动勉励和丈量技能,成功地确定了其固有频率(腔调),即实现了对纳米琴弦的演奏和拾音。在此根本上,人们逐渐调度样品环境的气体压强(这里以氪气(Kr)为例),使得吸附层的密度在压强浸染下缓慢增加。在恒温增压的过程中,一开始人们不雅观察到了琴弦的腔调缓慢、连续地低落。在靠近真空的压强下,这一征象可用于丈量气体原子的吸附过程,乃至能够分辨单个原子的吸附过程。
图6 Kr在单根碳纳米管表面吸附过程中纳米琴弦频率的变革。个中,灰度代表琴弦的振幅,实验温度为77 K
当压强连续增加时,人们创造在特定的温度和压强下,会不雅观察到一种特殊的征象:琴弦的腔调会骤然低落(图6)。这一征象解释琴弦的整体密度发生了不连续的、溘然的增加,而这一变革显然来自碳纳米管表面的吸附层:发生了一阶相变。这一过程可类比于封闭气缸内100℃、一个大气压的饱和水蒸气,当压强略微增加时,一部分气态水分子会凝集成液态,相应地这部分物质的密度显著增加。
图7 Kr在单根碳纳米管表面吸附过程中覆盖率的变革
对这一过程,人们还可以进一步作定量地剖析。由于相变是体系中大量原子的集体行为,因此发生相变时吸附层中的原子数量已经足够多到可以认为其均匀、完全地覆盖了整根碳纳米管。相变台阶的陡直特色也证明了这一假设:如果碳纳米管上不同区域的原子密度不同,发生相变的先后也会有所不同,不雅观察到的就不会是一个完全、陡直的台阶。基于这一假设,可以推导出整根碳纳米管加吸附原子层构成的琴弦具有均匀的线质量密度。由此可以写出琴弦频率(腔调)与线质量密度的关系:
个中,线质量密度由两部分构成:碳纳米管本身的密度和吸附原子层的密度。进一步,利用碳原子和吸附原子的质量,人们可以将吸附层与碳纳米管质量线密度的比值转换为原子数量的比值,并称之为覆盖率,即均匀每个碳原子之上吸附了几个气体原子,其表达式为
个中为吸附开始前的琴弦频率。如果利用这一表达式对图6中提取的频率数据进行处理,可以得到如图7所示的覆盖率—压强曲线。从这一曲线可以看到,在相变发生的位置,覆盖率有一个不连续的、显著的上升。更故意思的是,人们在某些特定的碳纳米管上不雅观察到了一个独特的台阶,涌如今1/6覆盖率的位置,即每6个碳原子恰好对应了一个吸附气体原子。这一覆盖率代表了吸附层中一种独特的相,如图8所示。在这种情形下,吸附层原子的晶格和其下方碳原子的六角形晶格具有公共的度规,故称之为“公度相(commensurate phase)”。
图8 Kr在单根碳纳米管表面形成公度相的示意图。个中,,为碳纳米管表面的晶格矢量,,为描述碳纳米管构造的“手性矢量”(chiralvector);,为吸附的Kr原子所构成单层晶体的晶格矢量
通过一系列实验,人们利用这样原子尺度的“琴弦”在低维吸附体系中,不雅观察到了多种不同相和相变以及超临界征象(即超临界干燥仪中用到的物理过程)。从这个意义上说,纳米尺度的“琴弦”能够帮助人们探索一些新奇的物理过程,算是一种物理学家喜闻乐见的“好乐器”。
5.2 用原子尺度的鼓膜来探索力学各向异性
各向异性指的是材料的物理特性随着方向而改变。在纳米材料中,一类范例的例子是二维层状晶体,其材料特性沿着原子层面内和面外的方向显著不同。对付常见的二维晶体,例如石墨烯、二硫化钼,其力学特性在面内是各向同性的,即只假如在原子层面内,无论沿着哪个方向,其弹性模量的值基本上没有变革。但并不是所有的二维层状材料都如此。以黑磷为例,其层内的原子排列呈现出波浪状的周期性起伏,犹如瓦楞板一样平常(图9)。因此,其面内两个方向上的弹性模量应该会显著不同,理论打算也证明了这一点。
图9 黑磷的晶体构造
但要从实验上不雅观察到力学各向异性却并不是一件刀切斧砍的事。丈量二维材料力学特性最标准也最常用的技能是纳米压印。详细方法是将二维材料固定在一个圆孔之上,用一个纳米针尖下压其悬空部分,从针尖测得的弹力—位移曲线中计算出悬空薄膜的弹性模量。然而这一技能无法分辨弹力中不同晶向弹性模量的分别贡献,因此无法分辨材料的力学各向异性。
乐器再一次给人们带来了独到的启示,设想一个鼓面,在不同频率的外力(例如声场)勉励下,可能会涌现不同的谐振模式。如果构成这个鼓面的材料具备一定的力学各向异性,是否有可能在不同的谐振模态中得到表示呢?更进一步,是否有可能通过全方位表征鼓面上不同模式的振动,来定量地反推出鼓面材料各个晶向的弹性模量呢?
图10 不同二维晶体构成的“小鼓”在振动模式描述(模态)和腔调(频率)上的差别。每个小圆盘代表了仿真所预测的振动描述:赤色代表振幅大,蓝色代表振幅小。右侧的十字代表了仿真模型中所用材料的弹性模量,双箭头越长则该晶向的弹性模量越高,各向同性模型中两个晶向的弹性模量相等(圆形虚线框)
沿着这样的思路,人们首先对此类器件进行了干系的仿真研究。如图10所示,当鼓面处在恰当的弹性区间(应力的影响可忽略不计)时,仿真结果显示,如果仅关注频率最低的谐振模态,将会很难分辨各向异性和各向同性的鼓面:振动的描述看上去险些千篇一律,仅仅由于弹性模量的高低而带来频率上的差异。但当人们开始关注更高的模态,就可以不雅观察到各向异性带来的影响。例如,第2和第3个模态具有高度相似的描述,其紧张差别是在空间上旋转了90°。在各向同性的鼓面上,这两个模态具有相同的频率,即涌现了简并;而在各向异性的鼓面上,这一简并征象消逝了,这是由于当振动方向在鼓面内旋转90°时,原来沿着较“软”晶轴的振动(模态2)变成了沿着较“硬”晶轴的振动(模态3),更大的回答力(更高的弹性模量)使得鼓面的频率也变高了。这一差别将是区分各向同性和各向异性鼓面的有力判据。如果人们不雅观察更高的模态,差异将会更加明显:各向同性的鼓面呈现出更高的旋转对称性。因此,通过不雅观察高阶模态的描述可以分辨鼓面材料的各向异性。
图11 实验不雅观测黑磷纳米小鼓中的各向异性。左侧为实验测得的每个振动模式的描述,右侧虚线为相对应的每个振动模式所测得频率。中间图标和菱形对应各向异性仿真模型(仿真参数在最下方)预测的振动模式描述与频率,与实验高度吻合。右侧为各向同性模型的预测,除最低的振动模式外均与实验差异显著(仿真参数在最下方)
在这个根本上,人们开展了相应的实验探索。在一个黑磷晶体构成的圆形鼓膜上,人们探测到了从低到高的一系列谐振峰,解释在这一频率范围内存在着多个谐振模式。利用“频率显微成像”技能,人们拍下了纳米小鼓中这些谐振模态的空间描述,就犹如拍下鱼洗中水面的纹理形状一样。从实验数据可以看出(图11),这些测得的模态和数值仿真给出的预测符合得很好。特殊值得把稳的是,个中的第2和第3个模态在频率上涌现了明显的差异。这一征象有力地证明了黑磷晶体中存在显著的力学各向异性。进一步,通过调度仿真模型中的材料参数,人们可以使仿真所得的模态以及每个模态的频率均与实验结果完美吻合。通过这一过程,人们成功地测定了黑磷中不同晶向的弹性模量,从而办理了各向异性二维材料力学特性的丈量难题。
可以看到,利用这种原子尺度“小鼓”开展的实验研究,可以揭示一些独特的材料特性,纳米尺度的“小鼓”对材料物理学家而言也可算是一件得心应手的“好乐器”。
6
结 语
从上文我们可以看到,乐器不仅在平时能够给物理学家带来放松和愉悦,还能够给物理学家带来研究中的启示。从更深的层次上来说,艺术和科学都是人类创造性的思维,也该当存在着一定的相通。以是从这样的角度来说,科学家也都是艺术家,在人类知识的殿堂中演奏着创新的乐章。
参考文献
[1] Feynman R P. J. Microelectromech. Syst.,1992,1(1):60
[2] Wang Z et al. Science,2010,327:552
[3] Wang Z et al. Nanoscale,2015,7:877
[4] Sazonova V et al. Nature,2004,431:284
[5] Bunch J S et al. Science,2007,315:490
[6] Cleland A N et al. Appl. Phys. Lett.,1996,69:2653
[7] Husain A et al. Appl. Phys. Lett.,2003,83:1240
[8] Li M et al. Nat. Nanotechnol.,2008,3:88
[9] Xu B et al. ACS Nano,2022,16(10):15545
[10] He R et al. Adv. Mater.,2005,17:2098
[11] Feng X L et al. Nano Lett.,2007,7:1953
[12] Fung W Y et al. Appl. Phys. Lett.,2009,94:203104
[13] Dai H et al. Acc. Chem. Res.,2002,35:1035
[14] Witkamp B et al. Nano Lett.,2006,6:2904
[15] Wu C et al. Nano Lett.,2010,10:1032
[16] Minot E D et al. Phys. Rev. Lett.,2003,90:156401
[17] Kong J et al. Nature,1998,395:878
[18] Hüttel A K et al. Nano Lett.,2009,9:2547
[19] Dzyubenko B et al. Nat. Phys.,2015,11:398
[20] Bai Y et al. Science,2020,369:1104
[21] Chen C et al. Nat. Nanotechnol.,2009,4:861
[22] Lee S et al. Appl. Phys. Lett.,2013,102:153101
[23] Chen C et al. Nat. Nanotechnol.,2013,8:923
[24] van der Zande A. M et al. Nano Lett.,2010,10:4869
[25] Lee J et al. ACS Nano,2013,7:6086
[26] Yang R et al. J. Vac. Sci. Technol. B,2014,32:061203
[27] Jia H et al. Nanoscale,2016,8:10677
[28] Lee J et al. Sci. Adv.,2018,4(3):eaao6653
[29] Steeneken P. G et al. 2D Mater.,2021,8:042001
[30] He R et al. Nano Lett.,2008,8(6):1756
[31] Zheng X et al. Appl. Phys. Lett.,2020,117:243504
[32] Eichler A et al. Nat. Nanotechnol.,2011,6(6):339
[33] Gouttenoire V et al. Small,2010,6(9):1060
[34] Xu Y et al. Appl. Phys. Lett.,2010,97(24):243111
[35] Aasi J et al. Nat. Photonics,2013,7(8):613
[36] Wang Z et al. Sci. Rep.,2016,6:28923
[37] Zhu J et al. Chin. Phys. Lett.,2023,40:038102
[38] Wang Z et al. Nat. Commun.,2014,5:5158
[39] Zhu J et al. Sci. China Inform. Sci. 2022,65:122409
[40] Davidovikj D et al. Nano Lett.,2016,16(4):2768
[41] Xu B et al. Small,2023,19:2300631
[42] Garcia-Sanchez D et al. Nano Lett.,2008,8:1399
[43] Garcia-Sanchez D et al. Phys. Rev. Lett.,2007,99:085501
[44] Tsioutsios I et al. Nano Lett.,2017,17:1748
[45] Nigues A et al. Nat. Commun.,2015,6:8104
[46] Migone A D et al. Phys. Rev. Lett.,1984,53(8):810
[47] Thomy A et al. Sur. Sci. Rep.,1981,1(1):1
[48] Lassagne B et al. Nano Lett.,2008,8:3735
[49] Chiu H et al. Nano Lett.,2008,8:4342
[50] Chaste J et al. Nat. Nanotechnol.,2012,7:301
[51] Wang Z. Phase Transitions on the Surface of Individual Nanotubes (Ph.D. Thesis). University of Washington/ProQuest Dissertations Publishing,2010,3431741
[52] Wang Z et al. Nano Lett.,2016,16(9):5394
[53] Wang Z et al. 2D Mater.,2015,2(2):021001
[54] Zheng X et al. Microsyst. Nanoeng.,2017,3:17038
[55] Wang Z et al. Sci. Rep.,2014,4:3919
来源:中国物理学会期刊网
编辑:尼洛














